El número áureo, la divina proporción o el número de oro es la relación que tienen entre sí dos segmentos de rectas. Esta construcción geométrica se encuentra presente en figuras, series numéricas, en formas de la naturaleza y en objetos creados por el ser humano.
Uno de los misterios del número áureo es que puede estar escondido en lugares muy diferentes y no siempre se tiene conciencia de que está presente. Se considera la proporción más estética que pueden contener las formas de la naturaleza y los objetos construidos por el hombre.
Contenidos
De Euclides a Fibonacci
Fue el matemático griego Euclides quien comenzó a estudiar formalmente el número dorado en su obra Elementos. Su definición del valor del número es: “una línea recta está dividida en el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor”.

Esta relación arroja un número irracional, porque es un número que no es resultado de la división de dos números enteros. Tiene infinitos decimales, es irrepetible, está representado con la letra griega phi, y se expresa con la cifra 1,6180339887498…
La letra phi se le adjudicó para honrar al escultor griego Fidias, creador del Partenón de Atenas, quien usó la proporción áurea para construir sus obras. Fue el matemático Mark Barr quien le adjudicó el símbolo en 1900.
Los griegos observaron algunos de los misterios del número áureo. Realizaron la primera construcción exacta de un pentágono regular empleando la regla y el compás. Además, usaron la divina proporción en construcciones y decoraciones.
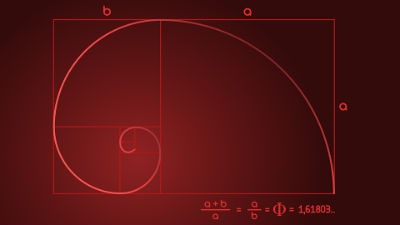
El número áureo guarda relación con la sucesión de Fibonacci, una serie infinita de números que se inicia con un 0 y un 1. Luego va añadiendo números de acuerdo con la suma de los dos precedentes (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…).
El resultado de dividir cualquier número de la sucesión de Fibonacci entre el que lo precede, es una cifra que se aproxima cada vez más al valor numérico de phi, 1,6180339887498… Nunca da igual, pero sí arroja un resultado por debajo o por encima de ese número.
Cuando se representa geométricamente el resultado aritmético, se obtiene la espiral o sucesión de Fibonacci, una de las imágenes características de la razón áurea.

Fascinación por la divinidad áurea
El término divina proporción fue acuñado por el matemático y teólogo italiano Luca Picioli en 1509. Entre las razones para considerarla divina es que al ser única, omnipresente e inconmensurable, es semejante a Dios.
Existen misterios del número áureo relacionados con la Biblia. Uno de estos es que las instrucciones que entregó Dios para construir el Arca de Noé y el Arca de la Alianza indicaban que usaran las proporciones 5×3. Son dos números de la sucesión de Fibonacci que arrojan como resultado 1,666.
La estrella pentagonal, símbolo de los seguidores de Pitágoras, también tiene relación con el número áureo, pues dentro de ella se encuentra el número phi. Se halla, por ejemplo, en la relación entre la diagonal y el lado del pentágono.
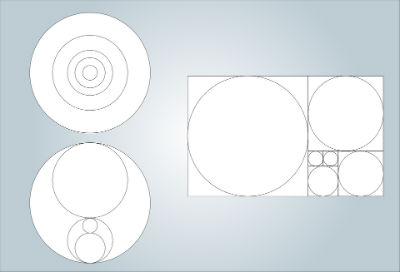
El número áureo en la naturaleza
Uno de los misterios del número áureo es que se encuentra con frecuencia en la naturaleza. Su característica es que siempre las formas de la naturaleza donde se encuentra guardan relación con la espiral de Fibonacci.
- En las nervaduras de las hojas de algunas especies de árboles.
- En el grosor de las ramas de los árboles.
- En los girasoles.
- En la proporción entre las abejas macho y hembra en una colmena.
- En la forma de las piñas que dan algunos árboles.
- En el número de espirales de numerosas variedades de flores y frutos.
- En el caparazón de un caracol.
- En huracanes y algunas galaxias.
En el cuerpo humano también puede encontrarse la proporción áurea. Se considera un ideal de belleza que la altura de una persona sea igual a la distancia entre las puntas de los dedos con brazos y manos totalmente extendidos. Esta distancia es igual a la que se obtiene al multiplicar 1,618 por la distancia que separa el ombligo del suelo.

La divina proporción en el arte y la arquitectura
La divina proporción ha sido utilizada por el ser humano en obras arquitectónicas y de arte:
- El dibujo Hombre de Vitruvio de Leonardo Da Vinci tiene proporciones basadas en el número áureo y es reconocido como un ideal de belleza. Da Vinci utilizó la proporción áurea en otras de sus obras como La Gioconda y La última cena. También lo hizo Miguel Ángel en El David y La Sagrada Familia, y Alberto Durero lo aprovechó para representar a Adán y Eva, entre otras obras.
- Otro tanto realizó Diego de Velázquez en su obra Las Meninas, y Salvador Dalí en su pintura Leda atómica. Dalí realizó esta obra basándose en la proporción áurea, pero usándola de tal manera que no es evidente a quien observa la pintura.
- Una escuela dentro del cubismo, la Sección de Oro, se dedicó a construir proporciones al descomponer una figura en cubos. Su máximo exponente fue Marcel Duchamp.
- La presencia del número áureo se advierte en los violines fabricados por Antonio Stradivarius entre los siglos XVII y XVIII.
También te puede interesar: ¿Qué son los fractales?
En la arquitectura, la divina proporción se encuentra en:
- El Partenón de Atenas.
- La Gran Pirámide de Gizeh.
- El Coliseo de Roma.
- La fachada de la Universidad de Salamanca.
- Las estructuras coloniales.
- La pirámide del Museo del Louvre en París.
- El edificio de las Naciones Unidas en Nueva York.
El arquitecto suizo Le Corbusier empleó el número áureo en sus diseños y creó el Sistema Modulor, basado en el número de oro. La sección áurea continúa siendo utilizada en la arquitectura de la actualidad.
¿Dónde más se encuentra el número áureo?
El número áureo está presente en objetos usados en la vida cotidiana, como las tarjetas de crédito o las cajetillas de cigarrillos. Ambas son ejemplos de rectángulos áureos.
El número áureo se encuentra también en algunas banderas. La bandera de Togo tiene la proporción entre el largo y el alto igual a phi.